Chapter 20 Testing Hypotheses About Proportions Reading Guide

A hypothesis is fabricated by the researchers about the data collected for whatsoever experiment or data prepare. A hypothesis is an assumption made by the researchers that are not mandatory true. In simple words, a hypothesis is a decision taken past the researchers based on the information of the population collected. Hypothesis Testing in R Programming is a process of testing the hypothesis fabricated by the researcher or to validate the hypothesis. To perform hypothesis testing, a random sample of data from the population is taken and testing is performed. Based on the results of testing, the hypothesis is either selected or rejected. This concept is known as Statistical Inference. In this article, we'll hash out the four-stride process of hypothesis testing, One sample T-Testing, Two-sample T-Testing, Directional Hypothesis, ane sample -test, two sample -test and correlation exam in R programming.

Iv Step Process of Hypothesis Testing

In that location are 4 major steps in hypothesis testing:

• State the hypothesis- This step is started by stating null and alternative hypothesis which is presumed as true.
• Formulate an assay plan and prepare the criteria for decision- In this pace, significance level of exam is set up. The significance level is the probability of a false rejection in a hypothesis test.
• Analyze sample data- In this, a test statistic is used to formulate the statistical comparison between the sample mean and the mean of the population or standard deviation of the sample and standard departure of the population.
• Interpret decision- The value of the test statistic is used to brand the decision based on the significance level. For example, if the significance level is set to 0.ane probability, and so the sample hateful less than 10% will be rejected. Otherwise, the hypothesis is retained to be true.

One Sample T-Testing

Ane sample T-Testing arroyo collects a huge corporeality of data and tests it on random samples. To perform T-Test in R, ordinarily distributed information is required. This examination is used to test the hateful of the sample with the population. For example, the height of persons living in an area is different or identical to other persons living in other areas.

Syntax: t.exam(x, mu)

Parameters:
x: represents numeric vector of information

mu: represents true value of the hateful

To know almost more optional parameters of t.test(), endeavour below command:

assistance("t.test")        

Example:

x <- rnorm (100)

t.examination (ten, mu = 5)

Output:

          Ane Sample t-exam  data:  x t = -49.504, df = 99, p-value < 2.2e-xvi culling hypothesis: true hateful is not equal to five 95 percent confidence interval:  -0.1910645  0.2090349 sample estimates:   mean of x  0.008985172        

Two Sample T-Testing

In two sample T-Testing, the sample vectors are compared. If var.equal = Truthful, the test assumes that the variances of both the samples are equal.

Syntax: t.examination(x, y)

Parameters:
x and y: Numeric vectors

Case:

x <- rnorm (100)

y <- rnorm (100)

t.test (x, y)

Output:

          Welch Two Sample t-test  data:  x and y t = -1.0601, df = 197.86, p-value = 0.2904 culling hypothesis: true difference in ways is not equal to 0 95 percent confidence interval:  -0.4362140  0.1311918 sample estimates:   mean of ten   mean of y  -0.05075633  0.10175478        

Directional Hypothesis

Using the directional hypothesis, the direction of the hypothesis tin be specified like, if the user wants to know the sample mean is lower or greater than another mean sample of the information.

Syntax: t.examination(ten, mu, alternative)

Parameters:
x: represents numeric vector information

mu: represents hateful against which sample information has to be tested

culling: sets the alternative hypothesis

Example:

x <- rnorm (100)

t.test (x, mu = 2, alternative = 'greater' )

Output:

          Ane Sample t-test  data:  ten t = -20.708, df = 99, p-value = ane alternative hypothesis: true hateful is greater than 2 95 per centum confidence interval:  -0.2307534        Inf sample estimates:  mean of x  -0.0651628        

I Sample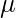-Test

This type of examination is used when comparing has to computed on one sample and the information is non-parametric. It is performed using wilcox.examination() function in R programming.

Syntax: wilcox.exam(x, y, exact = Naught)

Parameters:
x and y: represents numeric vector

exact: represents logical value which indicates whether p-value exist computed

To know nigh more optional parameters of wilcox.examination(), use below command:

assistance("wilcox.examination")        

Example:

x <- rnorm (100)

wilcox.test (x, verbal = False )

Output:

          Wilcoxon signed rank test with continuity correction  data:  x Five = 2555, p-value = 0.9192 culling hypothesis: true location is not equal to 0        

Two Sample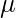-Examination

This test is performed to compare 2 samples of information.

Case:

ten <- rnorm (100)

y <- rnorm (100)

wilcox.examination (x, y)

Output:

          Wilcoxon rank sum test with continuity correction  data:  ten and y West = 5300, p-value = 0.4643 culling hypothesis: true location shift is non equal to 0        

Correlation Examination

This examination is used to compare the correlation of the two vectors provided in the office phone call or to test for the clan betwixt the paired samples.

Syntax: cor.test(x, y)

Parameters:
10 and y: represents numeric information vectors

To know about more optional parameters in cor.test() function, apply beneath command:

assistance("cor.test")

Example:

cor.test (mtcars$mpg, mtcars$hp)

Output:

          Pearson's product-moment correlation  data:  mtcars$mpg and mtcars$hp t = -6.7424, df = thirty, p-value = 1.788e-07 alternative hypothesis: true correlation is not equal to 0 95 percent conviction interval:  -0.8852686 -0.5860994 sample estimates:        cor  -0.7761684

huiepropis.blogspot.com

Source: https://www.geeksforgeeks.org/hypothesis-testing-in-r-programming/

Share this post